منطق سهگانهی بازیهای پازلی؛ معماها چگونه در بازیها طراحی میشوند؟

اگر بناست بازیهای پازلی ما را نسبت به چیزی به فکر وادارند، پس فکر دربارهی خود پازلها مثل فکر کردن دربارهی ماهیت خود فکر است. به عبارت دیگر، «برای حل پازلها چگونه منطق را به کار میبریم؟»
برای جواب به این سوال، در این جستار نشان خواهم داد پازلها در بازیهای ویدئویی چگونه میتوانند به سه مقوله در استدلالها تقسیم شوند، که در حوزههای منطق، ریاضی و فلسفه بسیار شناختهشده هستند:
- استدلال قیاسی
- استدلال استقرائی
- استدلال ربایشی
طراحی تمام انواع پازل در بازیهای ویدئویی مستلزم کاربرد یک یا چندتا از این نوع استدلالهاست تا بتوان حلشان کرد. این قاعده هم برای آن پازلهایی که ادامهدهندهی راههای همان پازلهای رومیزی سنتی هستند (مثل Gorogoa) صادق است و هم برای پازلهایی با مکانیسمهای کاملا نو و منحصربهفرد (مثل Baba is You).

چگونه میفهمیم که چطور میتوانیم در Limbo پیشروی کنیم، امتحاناتی که گلادوس جلوی راهمان میگذارد را حل کنیم، یا به معمای قتل در Return of the Obra Dinn پی ببریم؟ اگر خوب به آن فکر میکنید، متوجه میشوید بازیهای پازلی با انواع مختلفی از شیوهی فکری سروکار دارند. و برای همین بازیکنی که در لیمبوْ حرفهای است لزوما در حل معماهای سری Professor Layton یا Return of the Obra Dinn خوب نیست و بالعکس.
در واقع، سه بازیای که در بالا نام برده شد، به ترتیب، نمونههای خوبی در نمایش استدلال قیاسی، استقرائی و ربایشی هستند. برای همین، کسی که در استدلال قیاسی قوی است، لزوما در استدلال ربایشی قوی نیست و برعکس (با وجود اینکه همهی این انواع استدلالورزی نکات مشترکی دارند).
در بخش بعدی به این خواهیم پرداخت که این شیوههای استدلالورزی چه هستند و چگونه مصادیق آن را میتوان در برخی از پازلهای بازیها پیدا کرد.

پازلهای قیاسی (پازلهای منطقی)
استدلال قیاسی یک استدلال منطقی-ریاضیاتی است. یعنی، بیشتر توسط منطقدانها، فلاسفه، ریاضیدانها و دانشمندان علوم کامپیوتری استفاده میشود. این شیوهی استدلال، با الگوهای صوری سروکار دارد و نمادهایش میتواند علامتهای زبانی یا اشکال هندسی باشد. با این حال، خاصیت اصلی آنها را در بحثها میتوان یافت.
در منطق، وقتی میگوییم فلان برهانْ قیاسی است یعنی چون پیشفرضهایش صحیح هستند پس امکان ندارد نتیجهگیریاش غلط باشد. از این لحاظ، و با این فرض که یک برهان یا درست است یا نادرست، دیگر جایی برای تقریب باقی نمیماند؛ نتیجهگیری یک برهان قیاسی همیشه درست است چون بر پیشفرضهای درستی بنا شده.
استنباطهای قیاسی را بیشتر در پازلهایی که در قالب زبانهای طبیعی هستند میتوان شناخت. مثلا در پازل شماره ۲۹ بازی Professor Layton and the Curious Village:
پنج مظنون به مرکز پلیس برای بازجویی فراخوانده شدند. اینها گفتههای آنها بود:
A: یکی از ما پنج نفر دروغ میگوید.
B: دو نفر از ما پنج نفر دروغ میگویند.
C: من این آدمها را میشناسم، و سه نفر از ما پنج نفر دروغ میگویند.
D: به حرف هیچیک از آنها گوش نکن. از بین ما پنج نفر، چهار نفر دروغ میگویند.
E: هر پنج نفر دروغگوهای کثیفی هستند!
پلیس میخواهد تنها مظنونینی را آزاد کند که حقیقت را میگویند. پس چند نفر را آزاد خواهد کرد؟
اگر، هنگام فکر به سوال بالا، جواب فرد D را انتخاب کنید، پس گزینهی درستی انتخاب کردهاید. در صورتی که از روی هوا حدس نزده باشید، احتمالا برای رسیدن به این جواب از استدلال قیاسی استفاده کردهاید.
پیشفرضها چنین هستند:
۱. تنها پنج مظنون وجود دارد (A, B, C, D, E)
۲. در گروهی که در ۱ تعریف شد، همهی مظنونین تعداد متفاوتی از دیگر اعضای گروه را به دروغگویی متهم میکند (به ترتیب، از یک نفر تا پنج نفر).
۳. حداقل یک مظنون وجود دارد که حقیقت را دارد میگوید.
حال، میتوانیم با کمک فرضیهپردازی هم قیاس کنیم، یعنی فرضیهها را جلو ببریم تا ببینم کدامشان به نتیجهگیریهای عبث (متناقض) میرسد.
اگر حق با A باشد، پس کسی دارد دروغ میگوید. چه کسی؟ در این سناریو، فرد E باید دروغگو باشد، چون اگر حقیقت را گفته باشد، A نیز باید دروغگو باشد. اما d هم باید دروغگو باشد چون اگر حقیقت را گفته باشد، پس چهار دروغگو وجود دارند، که منطقا باید شامل A یا E هم بشود. بنابراین، اگر بیش از یک دروغگو در گروه وجود دارد، این با ادعای A به تناقض میخورد، و، بنابراین، نمیتواند او حقیقت را گفته باشد.
با دنبال کردن این روش فرضی برای تعلیق به محال/Reductio ad Absurdum،َ خیلی زود حاصل میشود: تنها کسی که ممکن است حقیقت را بگوید مظنون D است.

به عبارت دیگر، با نظر به اینکه پیشفرضهای ۱ و ۲ و ۳ صحیح هستند، غیرممکن است که نتیجهگیری ما اشتباه باشد. مشابه این مثال، چند بازی پازلی گرافیکی دیگر هم هست که از این استدلال قیاسی استفاده میکنند اما با کاربردهای متفاوت.
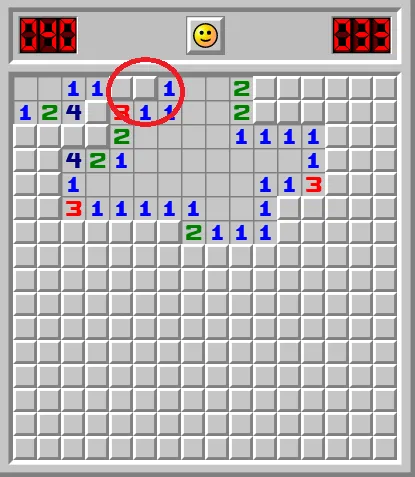
در سایر موارد، در بازیهایی مثل Minesweeper، گرچه بازیکن برای موفقیت باید خوششانس باشد، اما در بعضی موارد هم باید کمک قیاس میتواند نتیجه بگیرد بیشک در یک نقطهی فرضی بمب وجود دارد و نباید روی آن کلیک کند.
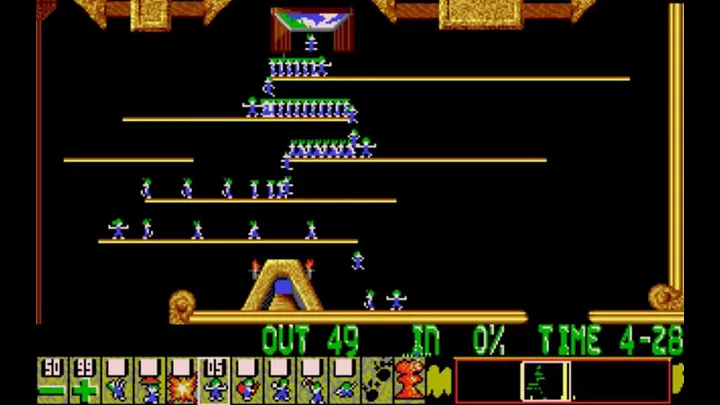
اما موارد دیگری هم هست که در آن بازیکن به شانس نیاز ندارد (مثلا در Baba is You)، اما در بعضی از بازیها، بازیکن باید در واکنش به موقع به مشکلات ماهر باشد. این مورد را در بازی کلاسیک Lemmings میبینیم، که در آن باید با فرمان دادن به واحدهای زیردستتان آنها را به مسیرهای امن ببرید.
در بعضی موارد، بازیهای پازل اکشن قیاسیای هم هستند که بیشتر روی چالشهای فیزیکی (مثلا واکنش بههنگام) تمرکز دارند و نه روی حل مشکلات منطقی که در آن زمانْ مسئلهای نیست. مصداق بارز آن تتریس است.
پازلهای خطی و غیرخطی
باید اشاره کرد، در خصوص Lemmings و تتریس، برای حل معماها راههای مختلفی وجود دارد. تمام راهحلها، بااینحال، از طریق پیشفرضهای درون مکانیسمهای بازی و لول دیزاین آن قابل استنباط هستند.
ویتنس/The Witness مثال خوبی است که آشکارا نشان میدهد میتوان پازلها را بهطور قیاسی به شیوههای متفاوتی حل کرد.
با استناد به «تفکیک مفهومی»/conceptual differentiation که Josh Bycer در مقالهاش به آن میپردازد، میتوانیم بگوییم پازلهایی که در Professor Layton and the Curious Village میبینیم «پازلهای خطی» هستند، و پازلی که در ویتنس میبینیم «پازلهای غیرخطی».
بااینحال، پازلهای غیرخطی قیاسی را به دو زیرمجموعهی دیگر میشود تقسیم کرد: آنهایی که روی کشف راهحلها متمرکزند و آنهایی که روی ابداع راهحل. این دوگانگی، که یکی کشفمحور است و دیگری ابداعمحور است، به خوبی توسط مارک براون/Mark Brown در جعبهابزار بازیسازان/Game Maker’s Toolkit تشریح شده است.
به عبارت دیگر، آنها پازلهایی هستند که علیرغم اینکه چند جواب برای یک مشکل واحد دارند، اما این راهحلها کشفشدنیاند (مثل ویتنس)، اما در سایر پازلها این خود بازیکن است که باید با ابزارهای موجود راهحل بسازد عوض اینکه خود سازنده راهحل را جایی پنهان کرده باشد. این نوع دوم از پازلهای غیرخطی را در پازلهای کدنویسیمحور/Coding Games میشود دید.

بازیهای کدنویسیمحور مثل برنامهنویسی هستند، یعنی برای رسیدگی به وظایف مختلف باید از الگوریتم استفاده کرد. این بازیها، بااینحال، گاهی آشکارا برنامهنویسیاند (مثل بازی Human Resource Machine)، اما گاهی هم زیرپوستیترند و مکانیسمهای متنوعتری دارند. مثل ترکیبهای شیمیایی و فیزیکیای که به ترتیب در Infinifactory و SpaceChem میبینیم.

این بازیها، با اینکه برخلاف Human Resource Machine مستقیما با کدنویسی سروکار ندارند، اما برای حل پازلها بازیکن باید قدمهایی را از پیش تعیین کند و سپس ادامهی فرآیند را اتوماتیک به خود بازی بسپارد.
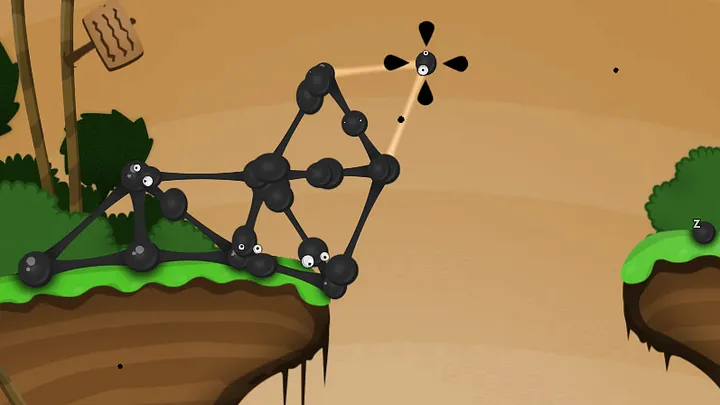
به یاد داشته باشید شرایط این بازیهای پازلی بسیار متفاوت از دیگر بازیهای پازلی است، حتی World of Goo، که در آن خود بازیکن باید قدم به قدم استدلالها را خودش جلو ببرد.
اما پازلهای غیرخطی، بهطورکلی، نقطهی مشترکشان این است که در آن راهحلهایی را کشف یا ابداع کرد که صرفهی اقتصادی ندارند [یعنی ممکن است لقمه را دور سر چرخاند. گرچه راهحلها همه مشکل را حل میکنند ولی بعضی راهحلهای سادهتر و دقت بیشتری دارند. در این پازلها، چیزی که با ۱۰ قدم میتواند حل شود را بازیکن ممکن است با ۴۰ قدم اضافیتر حل کند].
اما نباید فراموش کنیم تعدادی از بازیهای پازلی محتاج تفکر منطقی نیستند، لااقل نه آن منطق مرسوم قیاسیای که میشناسیم. در عوض، خیلی (و شاید اکثر) پازلها روی راهحلهای استقرایی یا ربایشی تمرکز دارند که در ادامه به آنها میپردازیم.
پازلهای استقرایی (آزمون و خطا/جستوجو)
برعکس قیاس، استقرا فرآیندی است که با آزمایش و راهحلهای کلی مشروط سروکار دارد، بنابراین نتایج بهدست آمده از استدلالهای استقرایی همیشه احتمال نقض شدنشان هست. از این لحاظ، حتی اگر یک استنباط صحیح استقرایی اکثر اوقات جواب دهد، باز هم زیاد پیش میآید با شرایطی مواجه شد که پیشفرضهای استدلال استقرایی صحیح هستند اما نتیجهگیریهایش غلط.
یک پازل را زمانی میتوان استقرایی یا حول آزمون و خطا در نظر گرفت که حل آن محتاج آزمایش مکانیسمها یا اشیای اطراف پازل باشد، یا با گمانهزنی، مشاهده، اعتبارسنجی و جستوجو.
احتمالا دوتا از زیرمجموعههای اصلی این سبک پازل پلتفرمها و پازل ادونچرها هستند.
پازل پلتفرمرهایی مثل Fez و Limbo در پرداخت به این قضیه پر از مثالهای بدیع هستند. در هر دو، بازیکن باید ابتدا محیط اطراف را با دقت بنگرد و فرضیههایی که در ذهن دارد را همزمان آزمایش کند (با مکانیسمهایی که بازی در اختیارش گذاشته، مثل پرید یا استفاده از برخی اشیای خاص).

مشابها، پازل ادونچرهایی که مکانیسمهای اشاره و کلیککردن/Point and Click دارند، مثل Gorogoa، Myst، و Machinarium، از بازیکن میخواهند که ابتدا صحنه را به دقت بررسی کند و بداند کجاها باید کلیک کند و در سر بزنگاه از کدام آیتم استفاده ببرد.
در هر دو مورد، پازل پلتفرمرها و پازل ادونچرها مشکلاتی را جلوی راه قرار میدهند که با روشهای استقرایی حلشدنی است، یا با آزمون و خطای محض یا از جز به کل رسیدن.
مثلا در Gorogoa، برخی از پازلها را یا بهطور کل یا حداقل بخشیاش را به زور آزمون و خطا میشود حل کرد، یعنی با صرف کلیکهای تصادفی روی تکههای مختلف تصویر بالاخره ممکن است مشخص شود فلان شی قابلتعامل و بدردبخور است. بااینحال، در طول زمان، هم در Gorogoa و هم در Limbo، Machinarium و سایر بازیها، میتوانیم بر اساس نمونههای جزئیای که قبلا دیدیم دست به نتیجهگیریهای کلی بزنیم (اینکه چه چیزهایی قابل تعاملند، کارکردشان چیست، و برای حل یک مشکل چه چیزهایی مفید و چه چیزهایی غیرمفیدند).

از این نظر، پازلهای قیاسی ممکن است شدیدا قابل پیشبینی و ساده شوند، مادامی که سازندگان هر دفعه شی، کارکرد، مکانیسم یا سناریوهای جدیدی وارد پازلها نکنند (اینگونه بازیکنان نمیتوانند هر دفعه به نتیجهگیریهای کلیای که کردند وابسته باشند و باید دوباره فرآیند آزمون و خطا و جستوجو را شروع کنند). در پازلهای ربایشی هم اتفاق مشابهی میافتد.
پازلهای ربایشی (تحقیقی)
برخی از منطقدانان بهدرستی میگویند استدلال ربایشی یا بهترین تبیین موجود یک نوع استدلال استقرایی است. اما ترجیح میدهم در بخش جداگانهای به این نوع استدلال بپردازم چراکه استفاده از آن در طراحی پازلها باعث تجربهی بهکل متفاوتی در گیمپلی میشود.
همانطور که در مثالهای دیگر در خصوص پازلهای استقرایی نشان دادیم، نتایج برآمده از استدلال ربایشی همیشه مشروط است [یعنی همهجا و هر زمان نمیتواند درست باشد] و از جز به کل میرسد. بااینحال، استدلالهای ربایشی شامل آزمون و خطا نیستند و از سنخ دیگری هستند.
استدلال ریایشی یعنی در بررسی علت وقوع یک پدیده (در یک مکان و زمان خاص) از بین گزینههای موجود، کدام گزینه از همه محتملتر است [برای همین نام دیگر این استدلال را «بهترین تبیین موجود» گذاشتهاند].
استدلال ربایشی اکثرا در بازیهایی استفاده میشود که بازیکن در نقش کارآگاه است، یا یک باستانشناس، وکیل، یا هر تیپ دیگری که معمولا کارش تحقیق روی جرم، یک راز و غیره است. بنابراین، این نوع استدلالورزی را بیشتر در بازیهای ادونچر میتوان یافت که در آن باید روی پروندههای جنایی تحقیق کرد. Disco Elysium و سری Ace Attorney مصداق بارز این قضیهاند.

اما یک مثال خیلی خوب از بازی پازلیای که زیاد از استدلال ربایشی استفاده میکند Return of the Obra Dinn است. در این بازی، بازیکن نقش ماموری از طرف کمپانی هند شرقی بریتانیا را دارد که باید روی خدمهی کشتی ابرا دین تحقیق کند، کشتیای تجاری که به مدت پنج سال گم شده بوده و زمانی که در سواحل انگلستان آمده همهی خدمهاش مرده بودند.
برای این تحقیق، بازیکن یک ساعت مخصوص دارد که زمان مواجهه با یک جسد، میتواند آخرین لحظات زندگی فرد متوفی را نشان دهد. از آنجا که نمیتوان با گذشتهی قربانی تعامل برقرار کرد، بنابراین فهم هویت آن خدمه، اینکه توسط چه کسی کشته شده، و چگونه کشته شده، مستلزم کلی استدلال ربایشی، و هر از گاهی، قیاسی است.
برای مثال: فرض کنیم جسدی تکوتنها در آن سوی دیوار چوبی و بیرون از کشتی پیدا شده است. سپس، وقتی آخرین لحظات زندگیاش را میبینید، صدای شلیکی که با دیوار برخورد میکند را میشنوید و متوجه میشوید شلیککننده ملوانی است آن «سوی» دیوار (درون کشتی). با استدلال ربایشی، نتیجه میگیرید محتملترین گزینه این است که قربانی بر اثر تیر غیرعمدی ملوان، کشته شده است.
باید به یاد داشت که این استدلال از جنس قیاس نیست چون پیشفرضهایی که بر اثر این مشاهده استنباط شدهاند حتما به این معنی نیستند که قربانی به این شکل مرده است: قربانی ممکن است بر اثر چیزی جز تیر مرده باشد (هیچ کالبدشکافیای انجام نشده)، و ملوان هم ممکن است عمدا مقتول را کشته باشد (یعنی یکجورهایی میدانسته قربانی در پشت دیوار ایستاده است).
البته، این پیشفرضها کمتر محتمل هستند اما غیرممکن هم نیستند. و حذف گزینههای کمتر محتمل و انتخاب محتملترین گزینه یعنی دقیقا روش استدلالهای ربایشی.
ترکیب انواع مختلف استدلاورزی در طراحی پازل
گرچه میتوان چند بازی پازلی دیگر هم که محتاج استدلال قیاسی هستند، یا استقرایی، یا ربایشی، دستهبندی کرد؛ نباید فراموش کنیم اکثر بازیهای پازلی، حداقل تا حدودی، ترکیبی از هر سه هستند.
مثلا در Braid، لحظاتی هست که باید مسئلهای قیاسی را حل کنید، اما برای رسیدن به قطعهی بعدی پازل باید تصاویر پازل را روی یک تصویر کنار هم بچینید ولی این به بازیکن توضیح داده نمیشود و خودش باید با آزمایشکردن (استقرا) نتیجه بگیرد. مشابها، در The Talos Principle هم بازیکن با استقراست که میآموزد چگونه ابزارهای موجود کار میکنند و سپس با کمک همانها پازلها را به شیوهی قیاسی حل کند.

وقتی صحبت بر سر ترکیب انواع مختلف منطق در پازلها باشد، شاید جالبترین موردش آنهایی باشند که اسمشان را «بازیهای پازلی کامل» گذاشتهام.
یک بازی پازلی کامل را میتوان بازیای تعریف کرد که نه فقط مسائلش، بلکه روایت و حتی مکانیسمهایش نیز باید همیشه استنباط شوند (خواه از طریق قیاس، یا استقرا و ربایشی). مصداق بارز آن ویتنس است.
پرواضح است که مثل سایر دستهبندیها، ویتنس تنها نمونهی موجود نیست (از Myst و Baba is You و خیلیهای دیگر هم میتوان نام برد)، اما برای توضیح مفهومی که میخواهم، ترجیح میدهم به ساختهی جاناتان بلو/Jonathan Blow ارجاع بدهم.
گرچه راهحلهای قیاسی برای حل پازلهای ویتنس وجود دارد، اما هیچیک از مکانیسمهای بازی برای بازیکن توضیح داده نمیشوند. پس الزاما با استقرا است که میتوان به معانی علامتها پی برد و از آنها برای حل پازل استفاده کرد و متوجه شد چه عناصری از سناریو را باید در قیاس خود بهعنوان فرض وارد استدلال کند.

حتی در پیرنگ نیز، ویتنس خود را با متن واضح و سخنرانیای توضیح نمیدهد. فهم همهی داستان به دوش استنباطهای بازیکن است که معمولا با کمک استدلالهای ربایشی به دست میآید. برای مثال، وقتی به شهری میرسید که ساکنین آن بر جای خود خشک شدهاند، ممکن است بهطور ربایشیْ استنباط کرد که بهخاطر عمل یکی از ساکنین که داشته سایهی خودش را در کنار چند سنگ روی زمین میدیده این اتفاق افتاده است.
در همهی طرق طراحی پازل، بازیهای پازلی پتانسیلشان برای توسعهی منطقهای سهگانه (استقرا، قیاس و ریایش) بسیار زیاد است.
همچنین فکر میکنم پتانسیل خلاقانهی بازیهای این سبکی نیز بالاست، گاهی حتی نبوغآمیز است. «بازیهای پازلی کامل» خصوصا از این جهت جالباند که بازیکن را غرق در جهانی میکنند که سراسر رازآلود است، جهانی که مسئلهای بزرگ درش هست و محتاج حلشدن است و تنها با کوشش فکری بازیکن میتواند حل شود.
بیگمان این سبک در آینده رازهای زیادی برای تحقیق، مکانیسمهای نو برای تست، و مسائل جدید برای حلشدن فراهم خواهد کرد. و من همیشه مشتاقم تا از آنها گرهگشایی کنم.
نویسنده: Vitor M. Costa
منبع: Superjump