درک مفهوم تقارن با استفاده از قضیه نوتر و پرندهای که برق او را نگرفت!

اگر به دههی 1920 در شهر گوتینگن آلمان برگردید، ممکن است در یک عصر گرم تابستانی، غوغای بحث و گفتوگو از آپارتمانی در فریدلندر را بشنوید. با یک نگاه اجمالی به پنجرهی اتاق، میتوانید گردهمایی دانشجویانی را مشاهده کنید که حول مسائل روز ریاضی حرف میزنند. با استراق سمع بیشتر ممکن است در نهایت صدای خندهی زنی را بشنوید که میزبانی این مهمانی را بر عهده دارد و او کسی نیست جز اِمی نوتر «Emmy Noether»، ریاضیدانِ نابغهای که قضیه نوتر را به جهان علم هدیه کرد!
در عصری که زنان از نظر فکری پایینتر از مردان تلقی میشدند، اِمی توانسته بود تحسین همکاران مرد خود را برانگیزد. چراکه چالشی دردسرساز در نظریهی نسبیت عام آلبرت انیشتین را حل کرد. درواقع او نظریهای ریاضیاتی و انقلابی را به جهان فیزیک هدیه کرد که رویهی مطالعهی جهان توسط فیزیکدانان را تغییر داد.
امی نوتر، زنی که چهرهی فیزیک را تغییر داد!
قضیه نوتر، قوانین پایستگی و تقارنها
نگاه جنسیتی در علم؛ از ماری کوری تا امی نودر
تقارنها از آن چیزی که فکر میکنید، مهمتر هستند!
نسبیت عام و قضیه نوتر
مروری بر زندگی امی نوتر
تقارنهای پیمانهای و قضیهی نوتر
امی نوتر، زنی که چهرهی فیزیک را تغییر داد!

حدودا یک قرن از روزی در 23 ژوئیه 1918 که قضیهی معروف نوتر به جهان علم معرفی شد، میگذرد، با این حال از اهمیت آن ذرهای کم نشده است. درواقع این قضیه همچون ستارهای راهنما برای فیزیکدانان قرن بیستم و بیست و یکم بوده و هست. نوتر یک ریاضیدان پیشرو در زمان خود بود و علاوه بر قضیهی معروف او که اکنون «قضیه نوتر» (Noether’s theorem) خوانده میشود، یک رشته در ریاضیات به نام جبر مجرد «abstract algebra» را هم راهاندازی کرد.

قضیهی نوتر در اوج زیبایی نشان میدهد که هر تقارن، میتواند کمیتِ معینی را حفظ کند؛ به عبارت دقیقتر به ازای هر تقارن در سیستم (وجود یک تابع متقارن و مشتقپذیر) کمیتی فیزیکی وجود دارد که ناوردا است. معادلهی بالا این مفهوم را بیان میکند که کمیت داخل پرانتز در طول زمان، تغییری نمیکند.
اما زندگی حرفهای نوتر با وجود چنین نبوغی چندان عالی پیش نمیرفت. او پس از اخذ دکترا مجبور شد سالها بدون دستمزد کار کرد. اگرچه او در سال 1915 در دانشگاه گوتینگن شروع به کار کرد، اما در ابتدا تنها به عنوان دستیارِ همکار مرد خود اجازهی تدریس داشت و تا سال 1923 هیچ حقوقی دریافت نمیکرد. ده سال بعد، با روی کار آمدن نازیها، نوتر توسط دولت مجبور به ترک شغل خود شد، چراکه نه تنها یهودی بود بلکه مظنون به عقاید سیاسی چپ هم بود.
پس از این اتفاق نوتر برای کار در کالج «Bryn Mawr» در پنسیلوانیا عازم ایالات متحده آمریکا شد؛ اما در کمتر از دو سال بعد، به دلیل عوارض ناشی از عمل جراحی در 52 سالگی درگذشت! در حالیکه اهمیت قضیه او به طور کامل شناخته نشده بود! اگرچه اکثر مردم هرگز نام امی نوتر را نشنیدهاند، اما فیزیکدانان همواره او را ستایش میکنند. در همین راستا روث گرگوری «Ruth Gregory»، فیزیکدان نظری در دانشگاه دورهامِ انگلستان، اذعان دارد که قضیهی نوتر در هر کاری که فیزیکدان مشغول به آن هستند، جاری است.
قضیه نوتر، قوانین پایستگی و تقارنها
نوتر ارتباط بین دو مفهوم مهم در فیزیک، یعنی قوانین پایستگی (conservation law) و تقارنها را مشخص کرد. به طور کلی قوانین پایستگی، مثلا بقای انرژی، بیان میکند که یک کمیت خاص همچون انرژی نه ایجاد میشود و نه از بین میرود بلکه همواره ثابت است. همین قطعیت در بقای انرژی هم به فیزیکدانان کمک میکند تا بسیاری از مسائل، از محاسبهی سرعت توپی که از روی تپه میغلتد تا درک فرآیندهای همجوشی هستهای را به خوبی حل کنند.
قانون پایستگی (اصل بقا) در فیزیک، بیانگر ثابت ماندن یک کمیت فیزیکی مربوط به یک سیستم مشخص در حین تحول آن سیستم است. تقارن در فیزیک، شامل ویژگیهای فیزیکی یا ریاضیاتی میشود که تحت برخی تبدیلها (مثلا چرخاندن) بدون تغییر باقی میماند.
از طرفی تقارنها توصیفکنندهی تغییراتی هستند که میتوانند بدون تغییر ظاهر یا عملکرد یک چیز اعمال شوند. به عنوان نمونه یک کره کاملاً متقارن است، چراکه اگر آن را در هر جهتی بچرخانید، باز هم شبیه به همان شکل اولیه، به نظر میرسد. همین توصیف تقارن قوانین فیزیک را هم در بر میگیرد. به این معنی که معادلات در زمان یا مکانهای مختلف تغییر نمیکند.

تصویری از اِمی نوتر که قضیه نوتر او در سال 1918 یکی از مهمترین تئوریهای فیزیک مدرن شد!
حال با توجه به توضیح این دو اصل مهم در فیزیک باید بدانید که قضیهی نوتر اذعان دارد که هر تقارنی دارای یک قانون بقای مرتبط و بالعکس (برای هر قانون بقا، تقارنی مرتبط وجود دارد!) است.
قضیه نوتر بیان میکند که هر تقارنی دارای یک قانون بقای مرتبط و هر قانون بقایی با یک تقارن مرتبط همراه است!
به بیان سادهتر، قانون بقای انرژی نشان میدهد که قوانین فیزیکیای که بر امروز حاکم است مانند دیروز است. به همین ترتیب، بقای تکانه (conservation of momentum) با این واقعیت مرتبط است که فیزیک در این قسمت از جهان، شبیه به هر جای دیگری در جهان است. این ارتباط بین تقارن و بقا، آشکارکنندهی وجود دلیلی در پشت ویژگیهای جهان هستی است که قبل از شناخته شدن آن رابطه، تصادفی به نظر میرسید!
جالب است بدانید که در نیمهی دوم قرن بیستم بود که قضیه نوتر پایه و اساس مدل استاندارد فیزیک ذرات (standard model) قرار گرفت. مدل استاندارد فیزیک ذرات به بررسی جهان هستی از دید زیراتمی میپردازد و همان مدلی است که وجود بوزون هیگز را پیشبینی کرد، ذرهای که با هیاهوی زیاد در سال 2012 کشف شد.
نگاه جنسیتی در علم؛ از ماری کوری تا امی نودر

زمانی که امی نوتر از دنیا رفت، آلبرت انیشتین در نیویورک تایمز نوشت: امی نوتر خلاقترین ریاضیدان نابغهای بود از زمان شروع تحصیلات عالی در بین زنان، تاکنون وجود داشته است. اگرچه این تعریفی صمیمی از جانب انیشتین است، اما ستایش انیشتین به جای اینکه بر برجستگی علمی امی در بین همکاران مردش باشد، به جنسیت او اشاره داشت!
به همین ترتیب، چندین ریاضیدان دیگر که به تحسین امی روی آورده بودند، در کنار آن تحسینها دربارهی ظاهر او اظهار نظر میکردند و حتی در یکی از این موارد در مورد زندگی جنسی امی هم اظهار نظرهایی شده بود! بنابراین همانطور که میبینید حتی کسانی که نوتر را تحسین میکردند، او را با معیارهای متفاوتی نسبت به مردان قضاوت میکردند.
تقارنها از آن چیزی که فکر میکنید، مهمتر هستند!

به طور کلی بحث تقارن از جمله موضوعات جذاب از گذشته تاکنون است. به عنوان نمونه برخی مطالعات گزارش میدهند که انسانهایی با چهرههای متقارنتر، زیباتر از چهرههای نامتقارن هستند. به این معنی که دو نیمهی صورت این افراد تقریباً تصویر آینهای یکدیگر (تقارن آینهای) است. از طرفی در اغلب موارد هنر، تقارن را به نمایش میگذارد، شما میتوانید با نگاهی به طرحها و کاشیهای ایرانی به خوبی این مساله را درک کنید. در کنار این موارد طبیعت هم تقارن را میپسندد؛ چراکه وقتی دانهی برف را 60 درجه بچرخانید، یکسان به نظر میرسد. در کنار آن گلبرگها، گلها، تارهای عنکبوت و بسیاری موارد دیگر با اصول تقارن شکل گرفتهاند.
اما در عین حال باید بدانید که قضیه نوتر مستقیماً در مورد این این مثالهای آشنا صدق نمیکند؛ به این دلیل که تقارنهایی که در اطراف خود میبینیم از نوع گسسته هستند، به این معنی که تنها برای مقادیری خاص صدق میکنند. به عنوان مثال، چرخش دقیقاً 60 درجه برای دانهی برف، از نوع گسسته است. به طور کلی تقارنهای مربوط به قضیه نوتر پیوسته هستند، به این معنی که اهمیتی ندارد چقدر در فضا یا زمان حرکت کنید، تقارنهای پیوسته، همواره حفظ میشوند و وابسته به مقادیری مشخص نیستند.
تقارنهای مربوط به قضیه نوتر از نوع پیوسته هستند و همچون تقارن دانهی برفی با گردش 60 درجه، گسسته به حساب نمیآیند.
در این میان یکی از انواع تقارنهای پیوسته، که به تقارن انتقالی «translation symmetry» معروف است، بر این اصل دلالت دارد که قوانین فیزیک با حرکت در کیهان تغییر نمیکند و به همان شکل باقی میماند.
قوانین پایستگی یا از جمله ابزارهای اساسی در فیزیک است. در کلاسهای فیزیک به دانشآموزان این اصل توضیح داده میشود که انرژی همیشه پایسته است. چراکه وقتی اولین توپ بیلیارد به توپهای دیگری برخورد میکند، انرژی حرکت اولین توپ در هنگام برخورد تقسیم میشود. بخش از انرژی توپهای دیگر را وادار به حرکت میکند، بخشی صدا یا گرما تولید میکند و مقداری از انرژی هم در توپ اول باقی میماند. در چنین حالتی، مهم نیست که چه اتفاقی میافتد، مقدار کل انرژی همیشه ثابت میماند. این موضوع در مورد تکانه هم صادق است.
به طور کلی این قوانین بهعنوان حقایقی غیر قابل انکار و صریح به دانشآموزان آموزش داده میشوند، اما لازم است بدانید که یک دلیل ریاضی پشت همهی آنها وجود وجود دارد. به گفته نوتر، بقای انرژی ناشی از تقارن انتقالی در زمان است. به طور مشابه، اصل بقای تکانه هم به دلیل تقارن انتقالی، در فضا است. پایستگی تکانه زاویهای، قابلیتی است که به پاتیناژکارها اجازه میدهد تا با در آغوش گرفتن بازوها، سرعت چرخش خود را افزایش دهند. این چرخش سریع از تقارن چرخشی (rotational symmetry) ناشی میشود و بیان کنندهی این است که با چرخش در فضا همهچیز به همان شکل اولیه خواهد بود.
در نظریه نسبیت عام انیشتین، هیچ حس مطلقی از زمان یا مکان وجود ندارد، بنابراین درک قوانین پایستگی در آن دشوارتر است، بنابراین طبق آنچه در ابتدای مقاله گفتیم، این همان جایی است که قضیهی نودر وارد میدان میشود و چالشهای پیشرو را کنار میزند.
نسبیت عام و قضیه نوتر
اگرچه نسبیت عام به عنوان یک نظریهی جدید و جذاب در سال 1915 به دنیا معرفی شد، اما وضعیت به گونهای بود که دیوید هیلبرت و فلیکس کلاین، ریاضیدانان آلمانی، غرق در ابهامات این دیدگاه جدید بودند. در همین راستا هیلبرت به منظور توسعهی ریاضیاتی نظریه، که گرانش را نتیجه انحنای ماده در فضازمان توصیف میکرد، با اینشتین در رقابت بود.
در همین حال و هوا بود که هیلبرت و کلاین به طور تصادفی با یک چالش جدید برخورد کردند. مسالهی پیشرو این بود که تلاش برای نوشتن معادلهای برای بقای انرژی در چارچوب نسبیت عام منجر به همانگویی یا توتولوژی «Tautology» میشد! به بیانی دیگر همچون نوشتن عبارتِ «0 برابر با 0»، معادلهی بقای انرژی در چارچوب نسبیت عام، هیچ اهمیتِ فیزیکی نداشت. این مساله غافلگیر کننده بود، چراکه هیچ نظریهی پذیرفته شدهای، قوانین پایستگی انرژیای به این شکل نداشت. بنابراین این دو ریاضیدان، امی نوتر را که در زمینههای مختلفِ ریاضیات تخصص ویژهای داشت استخدام کردند تا در گوتینگن به آنها بپیوندد و به حل معمای پیشرو کمک کند.
نوتر نشان داد که این قانون پایستگی عجیب، ذاتا به طبقهی خاصی از تئوریها که به طور کلی کوواریانت (Covariant) خوانده میشوند، تعلق دارد. در چنین نظریههایی، معادلات مرتبط با تئوری چه بهطور پیوسته و بدون شتاب یا با شتاب، در حال حرکت باشید؛ ثابت باقی میماند. زیرا در زمان حرکت، هر دو طرف معادلهی تئوری با هم تغییر میکند. در نتیجه نظریههای کوواریانت، از جمله نسبیت عام همیشه با این قوانین پایستگی غیر معمول همراه هستند؛ این کشف به عنوان قضیه دوم نوتر شناخته میشود. نوتر در راه اثبات قضیه دوم، اولین قضیه خود را در مورد ارتباط بین تقارنها و قوانین بقا را اثبات کرد و هر دو نتایج را در 23 ژوئیه 1918، در مقالهای به نام «Göttinger Nachrichten» منتشر کرد.
مروری بر زندگی امی نوتر
امی نوتر در سال 1882 به دنیا آمد و دختر دو ریاضیدان ماکس نوتر «Max Noether» و ایدا آمالیا نوتر «Ida Amalia Noether» بود. استعداد ریاضی امی جوان که با سه برادر خود در ارلانگن آلمان بزرگ شده بود در کودکی، آشکار نبود. با این حال، او به حل معماهایی که کودکان دیگر را سرگردان میکرد، معروف بود. در دانشگاه ارلانگن، جایی که پدرش در آنجا تدریس میکرد، زنان رسماً اجازه آموزش نداشتند، اگرچه میتوانستند با اجازه استاد کلاسها را به صورت استثنا شرکت کنند. زمانی که این قانون در سال 1904 تغییر کرد، امی نوتر به سرعت از آن استفاده کرد و دکترای خود را در سال 1907 گرفت.
نوتر به عنوان یک زن، حتی پس از استخدام در دانشگاه گوتینگن، برای گرفتن یک موقعیت آکادمیک همراه با دستمزد تلاش میکرد. اگرچه دانشگاه گوتینگن سرانجام در سال 1923 شروع به پرداخت حقوق به نوتر کرد، اما هرگز او را به عنوان یک استاد تمام عیار نشناخت! با این حال نوتر با شخصیت گرم و مهربانی که داشت خیلی زود مورد علاقهی همگان قرار گرفت. او عادت داشت که با دانش آموزان و همکارانش در حومه شهر پیادهروی طولانی داشته باشد و مناظره های طولانی و پرانگیزهای حول مباحث ریاضی برگزار کند. حتی نوتر گاهی دانشجویان خود را به آپارتمان خود میبرد و تا زمانی که بقایای دسر روی ظروف خشک میشد، صحبت و گفتوگوها ادامه پیدا میکرد. با توجه به همین تفاسیر هم مرگ او، در کمتر از دو سال پس از ورودش به جامعهی دانشگاهی در سال 1935، همگان را غمگین کرد.
تقارنهای پیمانهای و قضیهی نوتر
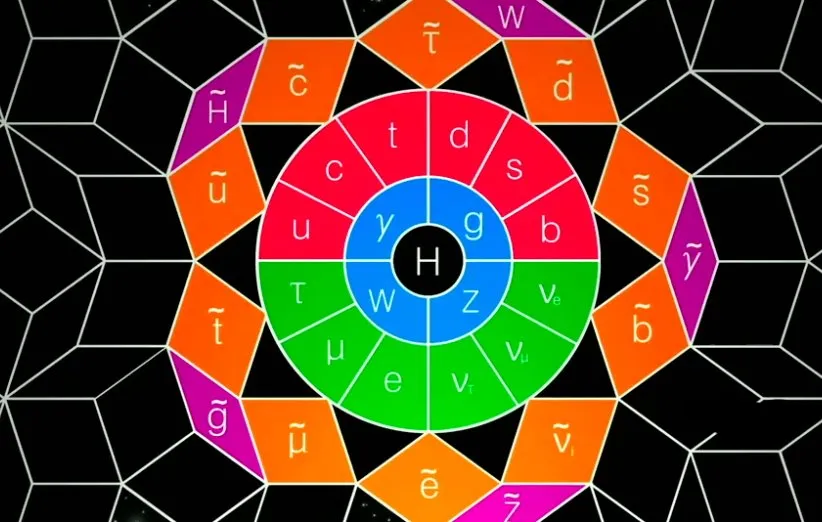
در دنیای فیزیک ذرات، تقارنهایی پنهانی با نام تقارنهای پیمانهای (gauge symmetries) وجود دارند که در دنیای الکترومغناطیس که منجر به بقای بار الکتریکی میشود، ظاهر میشوند. به طور کلی تقارن پیمانهای در تعریف ولتاژ الکتریکی به این شکل ظاهر میشود که ولتاژ (مثلا بین دو سر باتری)، نتیجهی اختلاف پتانسیل الکتریکی است. درواقع مقدار پتانسیل الکتریکی به خودی خود مهم نیست، بلکه اختلاف پتانسیل است که اهمیت دارد.
این توضیحات تقارن در پتانسیل الکتریکی را نشان میدهد، چراکه مقدار کلی پتانسیل الکتریکی بدون تأثیر بر اختلاف ولتاژ (اختلاف پتانسیل الکتریکی) قابل تغییر است. درواقع این همان مسالهای است که توضیح میدهد، چرا یک پرنده میتواند بدون برق گرفتگی روی یک سیم برق بنشیند، اما اگر همزمان دو سیم با پتانسیلهای الکتریکی متفاوتی را لمس کند باید با دنیا خداحافظی کند!
در دهههای 1960 و 1970، فیزیکدانان این ایده را گسترش دادند و تقارنهای پنهان دیگری مرتبط با قوانین پایستگی را برای توسعهی مدل استاندارد فیزیک ذرات پیدا کردند. بنابراین میتوان اینطور بیان کرد که توجه به قوانین پایستگی و ارتباط آن با تقارنها در فیزیک، دانشمندان مانند کسانی هستند که چکش به دست دارند و به دنبال میخاند. چراکه فیزیکدانان هر جا قانون بقایی را پیدا کردند، به دنبال تقارن هم هستند و بالعکس.
همچنین لازم است بدانید که توسعهی مدل استاندارد هم مدیون نودر و قضیهی مهمش است. مدل استاندار تئوری است که توسط ویلچک «Wilczek» به منظور توضیح تعداد زیادی از ذرات و برهمکنشهای بین آنها ارائه شد و او در سال 2004 جایزهی نوبل را به خاطر نقشش در توسعهی این مدل بُرد. مدل استاندارد در حال حاضر توسط بسیاری از فیزیکدانان به عنوان یکی از موفقترین تئوریهای علمی به دلیل توانایی آن در پیشبینی دقیق نتایج آزمایشها، در نظر گرفته میشود.
در همین راستا برخورددهنده بزرگ هادرونی (Large Hadron Collider) هم در جستجوی ذرات جدیدی است که با استفاده از بینش نوتر و قضیه نوتر پیشبینی شدهاند، چراکه یک تقارن پنهان فرضی، که ابرتقارن (supersymmetry) نامیده میشود، پشنهاد خواهر سنگینتری برای هر ذرهی شناخته شده را به جهان میدهد. البته با وجود امیدهای فراوان برای شناسایی این ذرات، تاکنون چنین ذراتی با توصیفاتی که در نظریهی ابرتقارن مطرح شده، یافت نشده است!
جمعبندی
فیزیکی که هر روز با آن سروکار داریم بر قضیه نوتر تکیه دارد؛ چراکه قوانین پایستگی که بارها در این مقاله به آن اشاره کردیم به توضیح سیستمهایی همچون امواج روی سطح اقیانوسها و جریان هوا بر روی بالهای هواپیما کمک میکند. درواقع شبیهسازی چنین سیستمهایی به فیزیکدان کمک میکند تا پیشبینیهایی در مورد الگوهای آب و هوا، ارتعاشات پلها یا اثرات انفجار هستهای داشته باشند.
علاوه بر اهمیت نوتر و قضیهاش در فیزیک، ایدههای این زن در ریاضیات نیز به قدری برجسته است که نام او به یک صفت در پس بسیاری از عناصر ریاضیات (همچون حلقههای نوتری، گروههای نوتری و ماژولهای نوتری) قرار گرفته شده است. در پایان باید خاطر نشان کرد که اگرچه امروزه زنان در علم، همچنان با چالشهایی روبرو هستند، اما هیچکس مجبور نیست برای دریافت دستمزد به خاطر کار علمیای که کرده است، مبارزه کند. این میراث اجتماعی امی نوتر است که با تلاشهای خود به ما هدیه کرد.
منابع اصلی:
A. Dick. Emmy Noether 1882-1935. Translated by H.I. Blocher. Birkhäuser, 1981.
منبع: ScienceNews

